この記事では高周波回路に関わるうえで知っておくべきデシベルの基礎知識について解説しています。 (作者:エンジャー)
デシベルとは
デシベル(dB)はある基準値に対して相対的な大きさを表すための単位です。電気回路に限らず多くの工学分野で使用されており、電圧、電力、音圧などの物理量のレベルを表現する際に使用されることが多いです。デシベルは対数を用いて表現されるため、非常に大きな値や非常に小さな値を扱う際に便利なことが特徴です。
dBの語源
dBのd(deci:デシ)はSI接頭語の一つで10分の1という意味を持ちます。B(bel:ベル)はアメリカの発明家アレクサンダー・グラハム・ベルにちなんだもので、電話の伝送損失を表すのにこの単位が用いられたことに由来しています。またdBの読み方は正式名称のまま「◯◯デシベル」と呼ぶこともあれば、少し省略して「◯◯デシ」と言ったり、アルファベットをそのまま「◯◯デービー」と呼んだりもします。
自然対数と常用対数の違い
対数には自然対数と常用対数の2つの種類が存在しますが、それぞれの基底が異なります。自然対数は、基底がネイピア数 e(約2.71828)で、その大きさは Loge(x)やln(x)というように表されます。この自然対数は物理学や数学の分野で使用されることが多いです。一方で常用対数は基底が10の対数で、デシが10分の1という意味からもわかるようにデシベルも常用対数です。常用対数はLog10(x)と表され、デシベルに変換する場合には10を掛けて10log10(x) [dB]と表されます。
常用対数の組み合わせ
 |
図1 常用対数の表現方法
常用対数の計算は難しそうなイメージがありますが、実務レベルでは5つの値の組み合わせさえ覚えておけば、暗算でデシベルの変換などができるようになります。この5つの値の組み合わせは以下のとおりです。
 |
図2 常用対数の代表的な組み合わせ
X=1のとき Log10(1) = 0 となり、デシベル表示は 10×0 = 0[dB]となります。同様にその他の値を計算するとLog10(2) ≒ 0.3、Log10(3) ≒ 0.48、Log10(5) ≒ 0.7、Log10(7) ≒ 0.85となり、デシベル表示にすると基準値に対して2倍のとき3dB、3倍のとき5dB、5倍のとき7dB、7倍のとき9dBとなります。また1と10は桁数が異なるだけで、計算自体は重複しているため10倍のときは10dBとなります。
デシベルの計算
デシベルは対数で表されているため、非常に大きい数値と非常に小さい数値同士で計算することも容易です。ここでは100,000と0.0001という2つの数値を比較する例で考えてみます。まずはそれぞれの2つの数値をそれぞれデシベルに変換します。
ここで2つのデシベル値の差を取ります。
すると両者には90dBの差があることが求まります。このように2つの数値をデシベルで表すことで、両者の関係性をわかりやすく数値化できます。
デシベルの活用例
ここでは分野別にデシベルの活用例を紹介します。
高周波回路
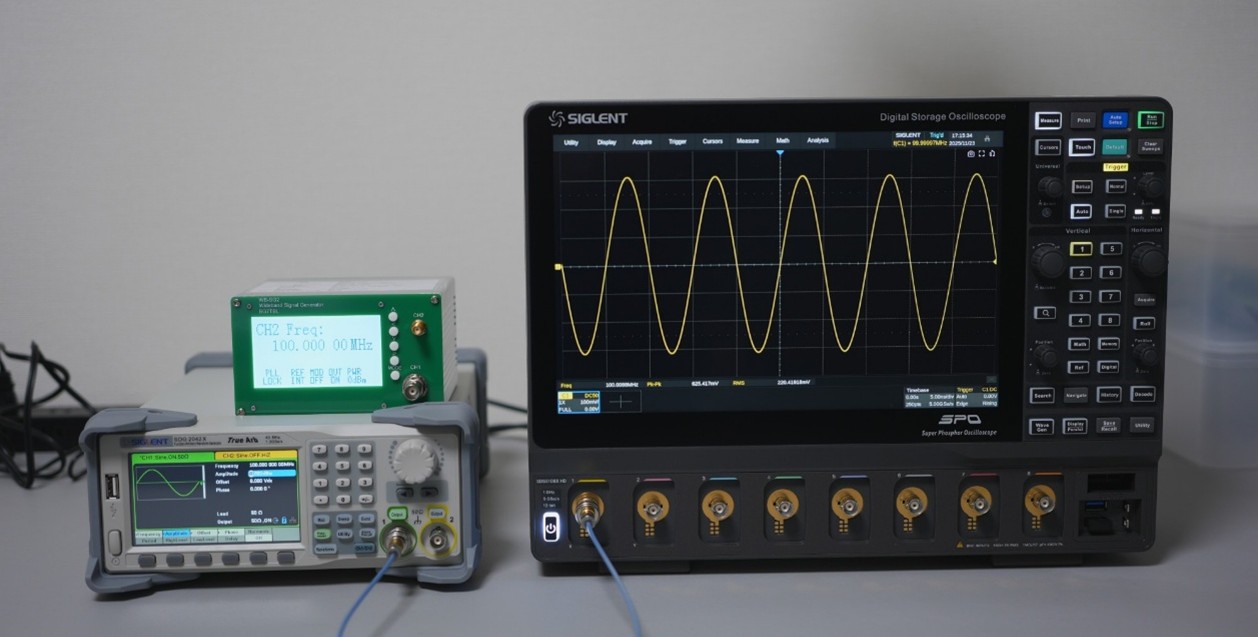
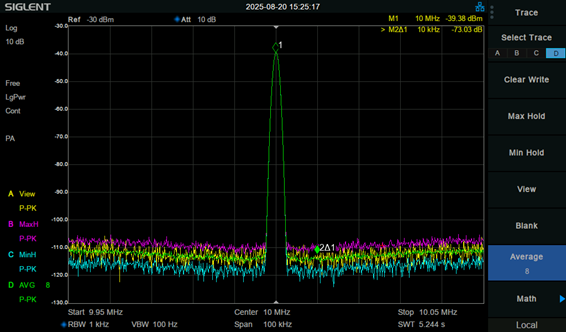
高周波回路では信号レベルをデシベルで表します。例えばアンテナやアンプのゲイン(Gain)、ケーブルやアッテネータによるロス(Loss)をデシベルとして扱うことで信号レベルを把握することが容易になります。下図の高周波回路の計測システムでは、各デバイスのゲインやロスをデシベルで表し電界強度を計算しています。
 |
図3 高周波測定でのデシベルの活用
ここではレシーバーの読み値、各デバイスのゲイン、ロスから電界強度を算出しています。式を見てわかるようにデシベルとして表記することで、各デバイスが高周波信号に対してどのような影響を与えているのかが非常に明確です。
音の大きさ
音響の分野では音の大きさを表すのにデシベルが使用されます。デシベルはある基準値に対して対数で値の大小を表現するものですが、音に関しては人間が聞き取ることができる最小の音圧を基準値、つまり0dBとしています。なおこの基準音圧を数値にすると20μPa(マイクロパスカル)と非常に小さな圧力変動です。また音は人間の耳によって近くできるため、人の感覚と音の大きさの関係性をデシベルで示すこともできます。具体的には以下のように規定されています。
- 0 dB:人間の聴力限界(最小可聴音)
- 20 dB:小さな寝息
- 30dB:ささやき声
- 40 dB:図書館の中
- 60 dB: 普通の会話
- 80 dB::交通騒音、掃除機の音
- 100dB:ガード下の電車の通過音
- 120dB:コンサート会場
- 140dB:飛行機のジェットエンジン
なお音圧のデシベルは常用対数に20を掛けて計算されます。つまり0dBと140dBは107=10,000,000倍の差があるということです。このようにデシベルを用いることで、広範囲の音圧を簡潔に表現でき、人間の感覚に適した形で音の大きさを評価することができます。
© 2024 T&Mコーポレーション株式会社