モーメント法(Method of Moments: MoM)は、電磁気学や音響学などの分野において、ヘルムホルツ方程式を数値的に解くための強力な手法です。特に、電磁波の散乱やアンテナの解析など、周波数領域における問題によく適用されます。
💡 ヘルムホルツ方程式とモーメント法
ヘルムホルツ方程式
電磁気学において、時間的に正弦波状に変動する電磁界(時間高調波、または周波数領域の電磁界)は、一般的にヘルムホルツ方程式によって記述されます。
 |
モーメント法の適用
ヘルムホルツ方程式自体は微分方程式ですが、MoMを適用する際には、この微分方程式を積分方程式の形に変換することが一般的です。電磁界解析で最もよく用いられるのは、以下のいずれかの積分方程式です。
-
電界積分方程式(Electric Field Integral Equation: EFIE)
-
磁界積分方程式(Magnetic Field Integral Equation: MFIE)
これらの積分方程式には、ヘルムホルツ方程式の自由空間グリーン関数がカーネル関数(積分核)として含まれています。このグリーン関数は、点源から放射される電磁波の伝搬特性を表します。
⚙️ MoMによる積分方程式の解法ステップ
MoMは、無限次元の関数空間で定義された積分方程式を、有限次元の線形連立方程式(行列方程式)に近似して解く手法です。
-
未知関数の展開(Basis Functions: 基底関数)
-
求めたい未知関数(例:導体表面上の表面電流密度 J)を、既知の基底関数(例:Rao-Wilton-Glisson (RWG) 関数など)の有限個の線形結合として近似的に表現します。
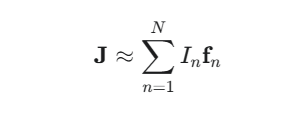
ここで、In が求めたい未知の係数(電流振幅)です。
-
-
テスト関数の導入(Testing Functions: テスト関数/重み関数)
-
展開された近似解を元の積分方程式に代入すると、誤差(残差)が発生します。
-
この残差を最小化するため、一連のテスト関数(Wm)を導入し、積分方程式の両辺とテスト関数との内積(積分)を取ります(これをガラーキン法と呼ぶこともあります)。
-
-
線形連立方程式の導出

-
連立方程式の解法
-
行列[Z]を逆行列計算や反復法(共役勾配法など)によって解き、未知係数Iを求めます。
-
求めたIを基底関数の展開式に戻すことで、元の未知関数(電流分布など)が得られます。
-
MoMは、特に導体(PEC)や誘電体の表面上の未知量(電流、電荷など)を解く場合に、離散化を表面のみに限定できる(体積全体を離散化する必要がない)という大きな利点があります。これは、FEMやFDTDなどの体積要素法と比較して、計算資源(メモリと時間)を節約できる主な理由です。
**モーメント法と有限要素法におけるガラーキン法
1. モーメント法 (MoM) におけるガラーキン法
電磁気学で使われるモーメント法では、未知関数(電流分布など)を基底関数 で展開し、テスト関数 も同じ基底関数 を選ぶ手法をガラーキン法と呼びます。
-
MoMの主な利点: 行列 が対称行列(またはエルミート行列)になりやすく、計算上の効率が良いこと。
2. 有限要素法 (FEM) におけるガラーキン法
構造解析や熱伝導、流体解析などで使われる有限要素法では、微分方程式を弱形式(変分原理に基づく積分形式)に変換した後、近似解の展開に用いる形状関数(Shape Function)を、そのまま重み関数としても使用します。
-
FEMでの利点: 剛性行列が対称行列になり、Ritz法(変分原理に基づく近似解法)と同じ結果を与えるため、Ritz-Galerkin法とも呼ばれます。FEMで最も一般的な定式化手法です。
3. ペトロフ・ガラーキン法 (Petrov-Galerkin Method)
ガラーキン法とは異なり、基底関数 とテスト関数 を異なる関数系で選ぶ手法をペトロフ・ガラーキン法と呼びます。流体計算の移流項のように、特定の現象で数値的な不安定性(振動)を抑えるために用いられます。




 T&M
即納ストア
T&M
即納ストア