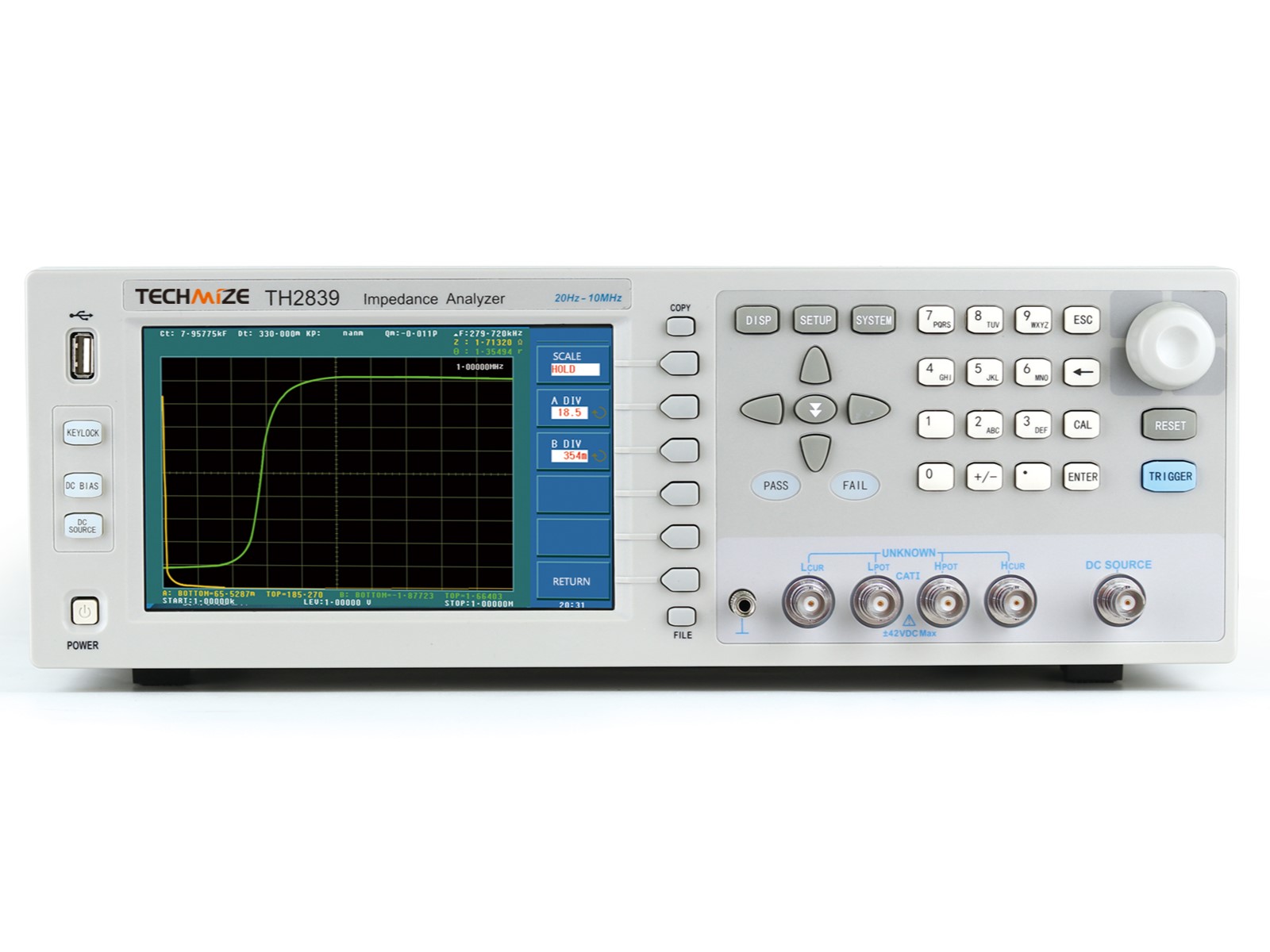
TechMize製インピーダンスアナライザTH2851-130の等価回路機能の使い方とその妥当性について解説します。

等価回路機能とは

インピーダンスアナライザは電子部品のインピーダンス特性を測定できる計測器です。加えて電子部品の電気的特性を簡略化し、回路モデルで表現する等価回路機能も備えています。この等価回路機能を用いることで、部品の特性を直感的に理解しやすくなるだけでなく、回路シミュレーションへの応用や部品選定の効率化にも繋がります。

 

等価回路とは

電子部品は抵抗(R)、コンデンサ(C)、コイル(L)といった基本的な要素の組み合わせることで、電気的な振る舞いを近似することができます。この近似的な回路モデルを「等価回路」と呼びます。

例えばコンデンサは、理想的な静電容量成分(C)だけでなく、微小な抵抗成分である等価直列抵抗ESR（Equivalent Series Resistance)や、微小なコイルンス成分である等価直列コイルンスESL（Equivalent Series Inductance)を含んでいます。これらはコンデンサのリード線や電極、誘電体の損失などに起因するもので寄生素子と呼ばれます。

 

この等価回路を用いることによって、実際の電子部品の複雑な周波数特性を単純なRLCの組み合わせでモデル化し、電気的挙動を理解しやすくすることができます。特に高周波領域では寄生素子の影響が顕著になるため、等価回路による部品評価が不可欠です。

 

等価回路トポロジー

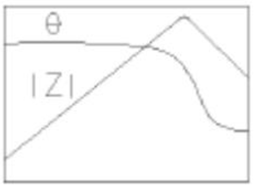
等価回路は対象とする電子部品のインピーダンス特性に応じて、様々な回路構成（トポロジー）が考えられます。TechMize製のインピーダンスアナライザTH2851-130には、代表的な電子部品の特性をモデル化するために、7つの等価回路トポロジーが内蔵されています。

 

A：RLC並列回路（3素子直列RLCモデル）

 

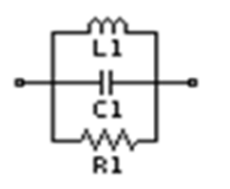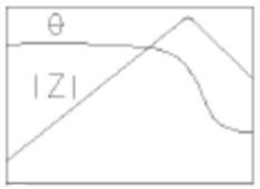この等価回路は抵抗(R)、コイル(L)、コンデンサ(C)がすべて並列に接続されたトポロジーです。周波数特性としては、特定の周波数においてインピーダンスが極大となる「反共振」を示します。共振周波数より低い周波数ではコイルLのインピーダンスが低く、高い周波数ではコンデンサCのインピーダンスが低くなるため、共振点から外れるとインピーダンスは低下します。共振時のインピーダンスの最大値は抵抗Rによって決まります。

主にコイルの等価回路モデルに使用されるもので、主となるコイルンスLに対し、コアの磁気損失を等価的な並列抵抗Rで、巻線間に存在する浮遊容量を並列容量Cで表現する際などに用いられます。

この等価回路モデルが実用的な周波数範囲は、対象とする部品の種類や構造に大きく依存しますが、共振現象を示す周波数帯域、あるいはDCから数MHz程度までのインピーダンス特性を近似するために使用されます。

 

B：RL直列 || C 回路 (3素子)

 

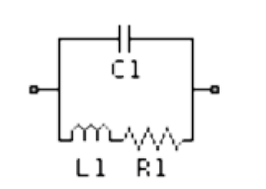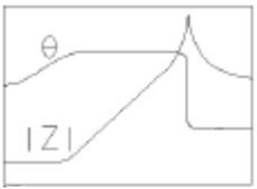この等価回路は抵抗(R)とコイル(L)の直列回路に対し、コンデンサ(C)が並列に接続されたトポロジーです。周波数特性としては、ある周波数で自己共振を起こしインピーダンスが最大となります。この自己共振周波数SRF（Self Resonant Frequency）より低い周波数帯では主にコイルとしての特性を示し（インピーダンスは周波数と共に上昇）、SRFを超えると並列Cの影響が支配的になります。また抵抗はリード線に起因するDC、また超低周波での抵抗値に相当します。

このトポロジーもコイルの等価回路モデルとして使用されますが、自己共振周波数におけるピークがより急峻で、低損失なコイルに適したモデルと言えます。

実用的な周波数範囲はコンデンサの寄生容量が影響を及ぼし始める領域で、コイルの種類によっては100MHz程度まで使用できることもあります。

 

C：RC並列 + L 回路 (3素子)

 

この等価回路は抵抗(R)とコンデンサ(C)の並列回路に対して、コイル(L)が直列に接続されたトポロジーです。周波数特性としては、低周波域では主に抵抗Rがインピーダンスを決定しますが、周波数が上昇するにつれて並列容量Cや直列インダクタンスLの影響が顕著になり、特定の周波数でLとCによる直列共振が発生します。抵抗値が低ければこのときのインピーダンスは最大、抵抗値が高ければインピーダンスは最小を示します。

主に高抵抗値を持つ抵抗器（数kΩ以上）の高周波特性を表現するために用いられます。この場合、Rは抵抗器の主抵抗値、Cはその抵抗器の端子間や内部構造に起因する寄生容量、Lは抵抗器のリード線や内部導体のインダクタンスを表します。

このモデルが実用的な周波数範囲は、DCから抵抗値が浮遊容量Cによって影響を受け始める周波数、具体的には数MHz程度までです。

 

D：RLC直列回路（3素子）

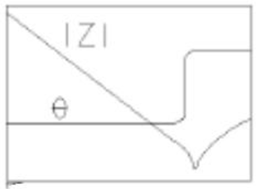この等価回路は、抵抗(R)、インダクタ(L)、コンデンサ(C)がすべて直列に接続されたトポロジーです。特定の周波数においてLとCのリアクタンスが打ち消しあい、インピーダンスが抵抗Rのみとなって最小値を取ります。共振周波数より低い周波数ではCのインピーダンスが支配的で、高い周波数ではLのインピーダンスが支配的となります。

一般的にコンデンサの特性を表現するために用いられ、Cは主容量、Rは等価直列抵抗(ESR)、Lは等価直列インダクタンス(ESL)を表します。

DCから部品の自己共振周波数およびそれ以上の周波数帯で実用的であり、特にコンデンサのESRやESLが問題となるスイッチング電源のデカップリング用途や、フィルタ回路の解析などで広く用いられます。

 

E：RLC直列 || C 回路 (4素子)

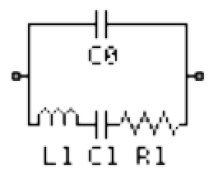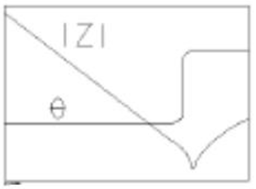この等価回路は、抵抗(R1)、インダクタ(L1)、コンデンサ(C1)の直列回路に対し、コンデンサ(C0)が並列に接続された構成です。周波数特性としてはRLC直列回路によってンピーダンスが最小となる直列共振周波数(f_s)を持ち、さらに高い周波数では並列容量C0との組み合わせによってインピーダンスが最大となる並列共振周波数（f_p）を持ち、f_sとf_pが非常に近接した周波数に存在するのが特徴です。

主に水晶振動子やセラミック発振子といった圧電振動子の電気的特性を非常に良く表現します。L1はモーショナルインダクタンス、C1はモーショナルキャパシタンス、R1はモーショナル抵抗、C2は電極間容量やパッケージ容量などの並列容量に相当します。

振動子の基本波の共振周波数、およびその近傍の周波数（通常、数kHz～数百MHz）まで実用的で、発振回路の設計やフィルタの解析に活用されます。

 

F：RLC並列 + R 回路 (4素子)

この等価回路は、抵抗(R1)、インダクタ(L1)、コンデンサ(C1)の並列回路に対し、抵抗(R0)が直列に接続されたトポロジーです。周波数特性としては、R1, L1, C1からなる並列共振回路部の反共振によって高いインピーダンスを示します。またDC付近の低い周波数のインピーダンスは抵抗R0とR1によって決まります。

電磁波吸収体や一部のノイズ対策部品のように、特定の周波数で高いインピーダンスが要求されるがDC的にはある程度の導通が必要な複雑なインピーダンス特性を持つ部品の等価回路モデルとして使用されます。

特に共振特性とDC抵抗特性を同時に考慮する必要がある場合に有効で、数MHz程度の比較的高い周波数まで実用性の高いモデルです。

 

G：RL直列 + RC並列 回路 (4素子)

 

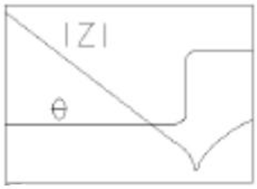この等価回路は、抵抗(R1)とインダクタ(L1)の直列回路に、抵抗(R2)とコンデンサ(C2)の並列回路がさらに直列に接続されたトポロジーです。周波数特性は、RL部分とRC部分の時定数が異なるため、周波数によって支配的な要素が変化し、複数の変曲点を持つ複雑なインピーダンス特性となります。低周波ではL1のインピーダンスが小さく、C2のインピーダンスが大きいため、主にR1とR2の抵抗成分がインピーダンスに寄与します。高周波ではL1のインピーダンスが増大し、C2のインピーダンスが減少するため、これらの相互作用によりインピーダンスが形成されます。

フェライトビーズや積層セラミックコンデンサ(MLCC)の精密モデル、あるいはバッテリーの内部インピーダンスなど、複数の物理現象が絡み合う部品を表現するのに用いられます。

このモデルは、低周波から高周波まで非常に広帯域な周波数範囲で実用的で、特に複数の緩和現象や分散特性を持つ材料・部品解析などで活用されます。

 

 

等価回路機能の使い方

インピーダンスアナライザTH2851-130では等価回路機能を使用することで、測定したインピーダンスデータから等価回路モデルの各素子値を自動的に算出することができます。ここでは基本的な使い方について紹介します。

 

等価回路機能（Equivalent Circuit）

等価回路機能はAnalysis→Equivalent Circuitから呼び出すことができます。

 

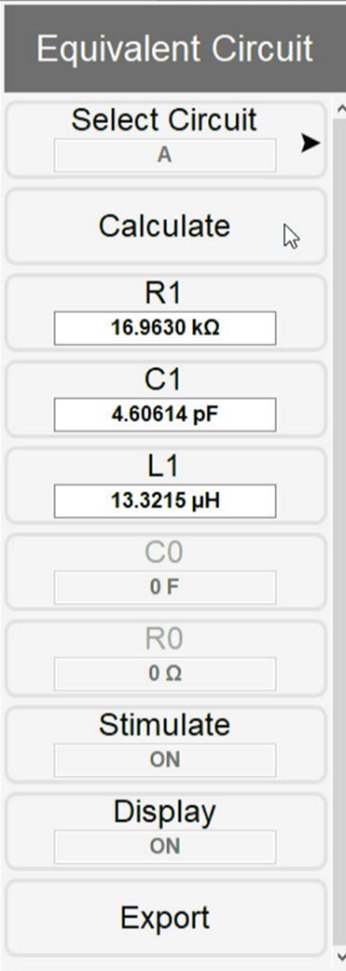回路トポロジーの選択

Select Circuitで7つの回路トポロジーから適切なものを選択します。なおどのトポロジーが適切かわからない場合は、下図のExample of DUTを参考にしてみても良いです。

 

定数の計算

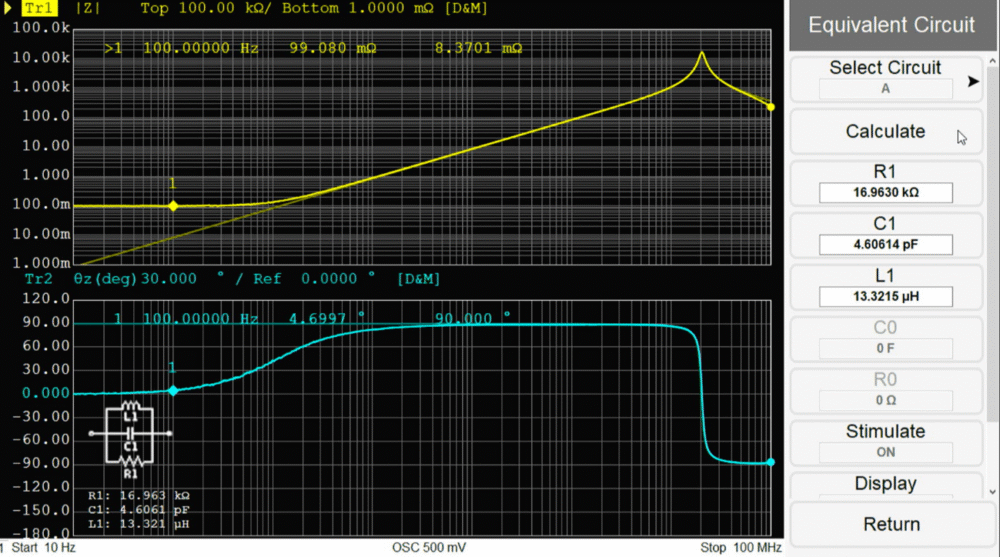
回路トポロジーを選択した状態でCalculateを押すと、等価回路の各定数が自動で計算されます。ここでは等価回路モデルAの抵抗R1が16kΩ、静電容量C1が4.6pF、インダクタンスL1が13.3uHと求まっています。

 

 

等価回路の表示設定

SimulateをONにすると等価回路のインピーダンス特性がグラフ上に薄い線で表示されます。実測と等価回路を比較してみると、1kHz以下の低い周波数で乖離が見られるものの、1kHz以上の周波数範囲では実測と等価回路がほぼ一致していることが確認できます。このように等価回路の妥当性を即座に確認できるのはTH2851のメリットです。

またDisplayをONにするとグラフ画面の左下に等価回路とともに各素子の定数が図として表示されます。これも等価回路の状況が視覚的に理解できるため非常に便利です。

 

等価回路データの保存

Exportではテキスト（txt）形式で等価回路の定数を出力できます。データを画像として保存する場合は不要ですが、メモとして等価回路データを残したい場合に有効な機能です。

 

等価回路機能の妥当性

実際に様々な抵抗、コイル、コンデンサのインピーダンス特性を測定し、等価回路機能の妥当性について検証してみます。

 

抵抗

抵抗は1Ω、100Ω、100kΩの酸化金属皮膜抵抗と100Ωのセメント抵抗の等価回路を算出してみます。なお等価回路のトポロジーはBとCを用います。

 

酸化金属皮膜抵抗1Ω、トポロジーB

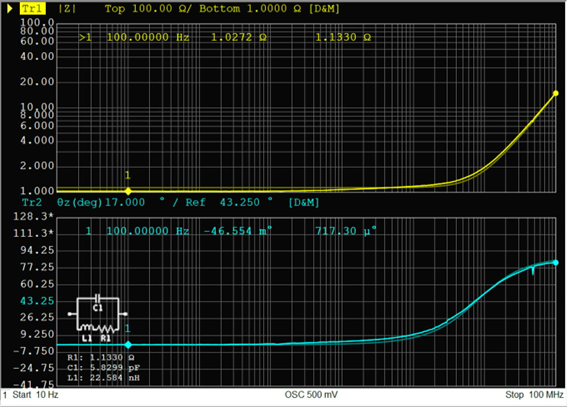上側のインピーダンス特性で実測と等価回路を比較すると、100Hzにおいて実測が1.0272Ωに対して等価回路が1.1330Ωと10%程度の誤差があるものの、周波数帯域全体で見ると概ね一致しており、十分実用的なレベルと言えます。

 

酸化金属皮膜抵抗1Ω、トポロジーC

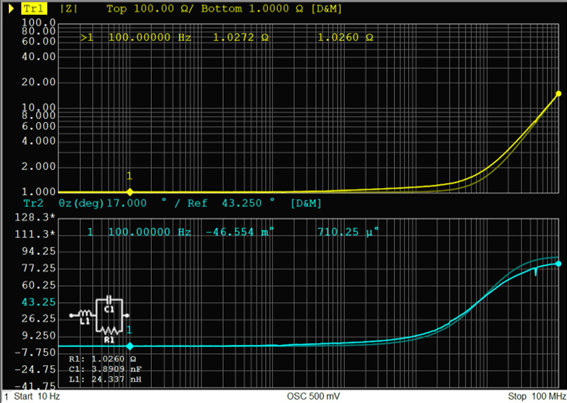トポロジーCも全体的な傾向は概ね一致していますが、寄生インダクタンスの影響が出はじめる100kHz以上の周波数帯において、実測と等価回路の差がトポロジーBよりも大きくなっています。そのため今回のケースでは、低抵抗の部品に対してはトポロジーBのほうが向いていると言えそうです。

 

酸化金属皮膜抵抗100kΩ、トポロジーB

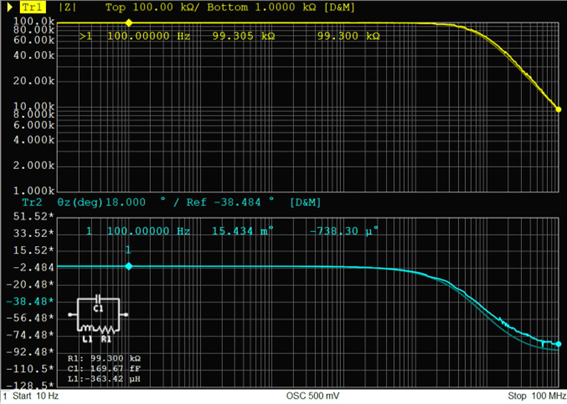100kΩの実測と等価回路を比較すると、インピーダンス特性はほぼ完璧に一致していることが確認できます。下側の位相特性で比較すると1MHz以上の周波数で若干の差が生じていますが、ほとんど無視できるレベルです。

 

酸化金属皮膜抵抗100kΩ、トポロジーC

トポロジーCはインピーダンス特性だけでなく、位相特性までも全周波数帯で概ね一致しています。このことから高抵抗の部品に対してはトポロジーCの方が適切と言えそうです。いずれにしても等価回路機能の有効性が見て取れます。

 

酸化金属皮膜抵抗100Ω、トポロジーB

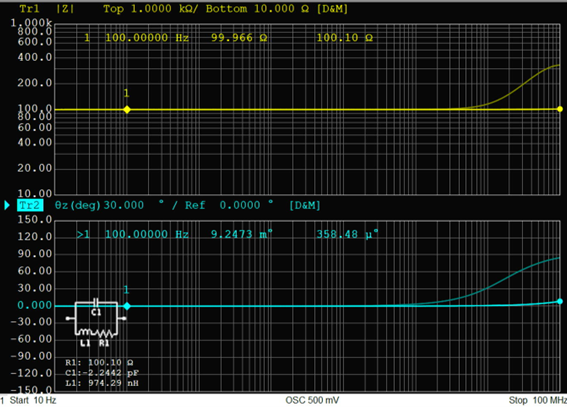TH2851では100Ωの抵抗を用いてキャリブレーションを行うため、100Ω周辺の測定精度が最も高くなります。その中で100Ωの酸化金属皮膜抵抗は10Hz～100MHzの全周波数にわたってインピーダンスがほとんど変化せず、一定の値を示し続けています。一方で実測と等価回路のインピーダンス特性を比較すると、等価回路は10MHzあたりからインピーダンスが上昇し始めており、周波数が高くなるに従ってその差が大きくなっています。このように同じ酸化金属皮膜抵抗でも抵抗値によって有効周波数範囲に違いが生じるというのが、等価回路を使いこなすうえで難しいポイントの1つです。

 

セメント抵抗100Ω、トポロジーB

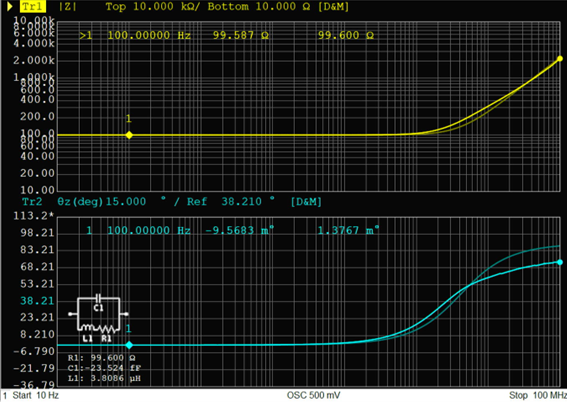同じ100Ωの抵抗でも抵抗の種類が異なると、実測と等価回路の関係も変化します。セメント抵抗は巻線抵抗をセメントでケーシングしたものですが、巻線抵抗が持つ寄生インダクタンスESLが大きいため、比較的低い周波数からインピーダンスが上昇し始めます。ここでは実測と等価回路のどちらも1MHzあたりからインピーダンスが上昇しており、等価回路の精度としては全周波数帯域で十分実用的と言えます。このように抵抗の種類、材質、構造によって妥当性が変化するのも、等価回路の面白くも難しいポイントです。

 

コイル

ここでは10uHの巻線インダクタをもとに、回路トポロジーによる等価回路の精度の違いを比較してみます。なお等価回路のトポロジーはAとBとFを用います。

 

巻線インダクタ10uH、トポロジーA

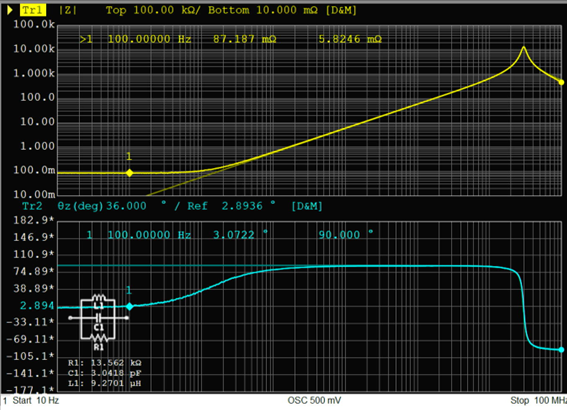トポロジーAは1kHz以下の低い周波数が適切にモデル化できてませんが、それ以上の周波数帯では実測と等価回路にほどんどさがなく、完璧と言って良い精度でモデル化できています。そのため実用上は問題なく使用できます。

 

巻線インダクタ10uH、トポロジーB

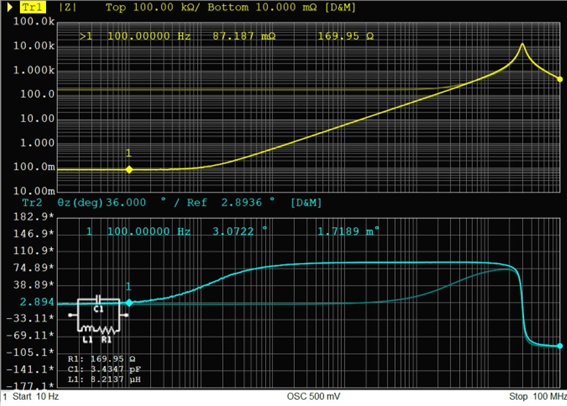トポロジーBは直列抵抗R1が170Ωと高い値となっているため、1MHz以下の周波数で実測と等価回路の差が非常に大きくなっています。そのため実用上は不適切なモデルとなります。

 

巻線インダクタ10uH、トポロジーF

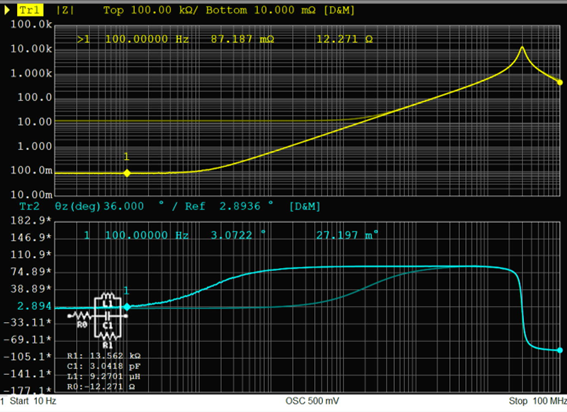トポロジーFもトポロジーBと同様に直列抵抗R0が12Ωと高い値を示しているため、100kHz以下の周波数で実測と等価回路の差が大きくなっています。このトポロジーFではトポロジーAの定数に対して直列抵抗R0の値を適切に設定すれば、実測と等価回路をほぼ一致させることも可能ですが、自動計算がうまくいっていないようです。

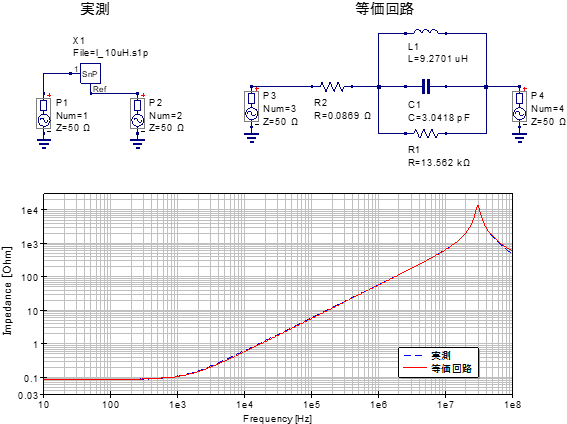このあたりは部品の種類や周波数特性によって得意・不得意があるのかもしれません。

 

コンデンサ

ここでは10uFの電解コンデンサと積層セラミックコンデンサをもとに、回路トポロジーによる等価回路の精度の違いを比較してみます。なお等価回路のトポロジーはDとGを用います。

 

電解コンデンサ10uF、トポロジーD

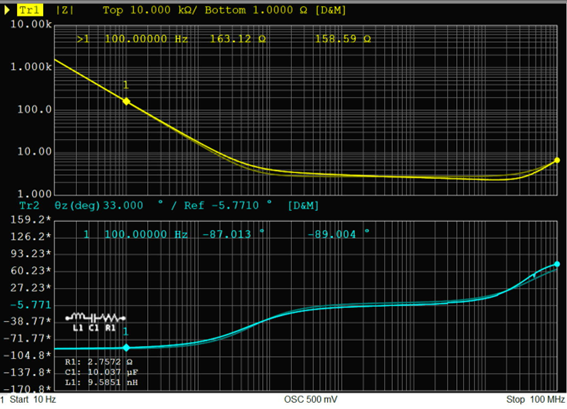電解コンデンサのインピーダンス特性は通称バスタブ特性と呼ばれるように、インピーダンスが下がり切るとその値を維持し続け、バスタブのような曲線を描きます。ここでは10kHzあたりから3Ω程度を維持し続け、30MHzあたりから上昇に転じています。そしてトポロジーDの等価回路においても概ね同様の特性を再現できており、十分実用に耐える等価回路モデルと言えそうです。

 

電解コンデンサ10uF、トポロジーG

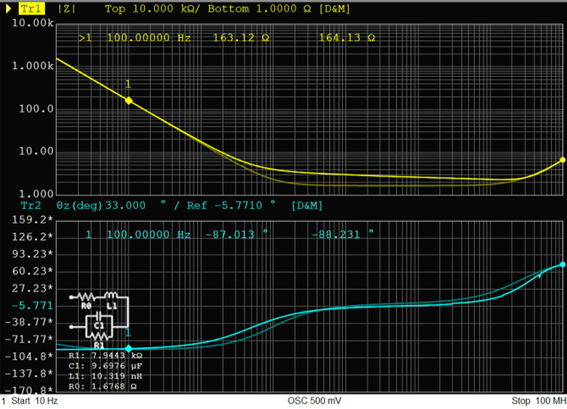トポロジーGはトポロジーDよりも素子数が1つ多いものの、10kHzあたりで実測と等価回路の差が大きくなっています。実用性という面では問題ないレベルですが、高い精度を求めるならトポロジーDを採用するほうが良さそうです。

 

積層セラミックコンデンサ10uF、トポロジーD

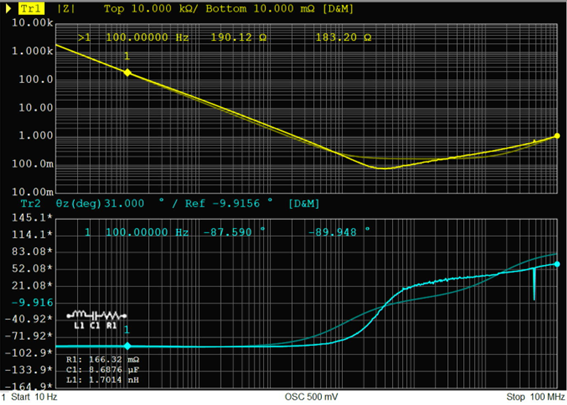同じ10uFでも積層セラミックコンデンサと電解コンデンサではインピーダンス特性が大きく異なります。その中でトポロジーDの等価回路は共振周波数あたりで実測の差が大きくなっています。この理由としては自己共振周波数以上のインピーダンスの上昇が若干緩やかなことが挙げられ、少ない素子数での再現が難しいポイントです。そのため実用上は精度をある程度妥協してそのまま使用することが多いです。

 

積層セラミックコンデンサ10uF、トポロジーG

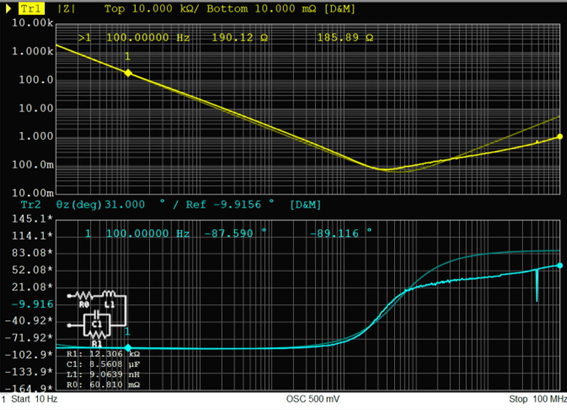トポロジーGとはトポロジーDと比較して、自己共振周波数あたりの精度が高くなっています。そのかわりに10MHz以上の周波数が高い領域で実測との差が大きくなっており、どの周波数帯を重視するかによって適切なモデルが変わってくることがわかります。トポロジーGも精度面で少し物足りないものの、実用上は問題なく使用可能です。