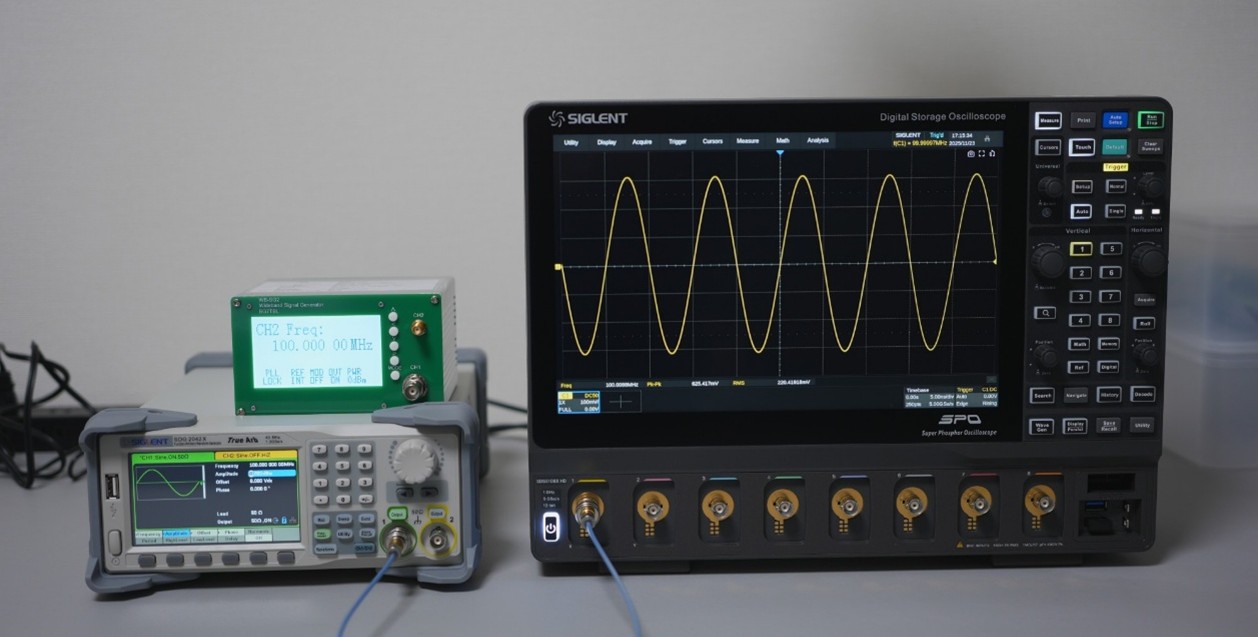
エンジャーさんよりこの記事ではファンクションジェネレータ（SDG2042X）から出力された信号に対するオシロスコープ（SDS804X）とスペクトラムアナライザ（SVA1015X）の波形の見え方の違いについて解説しています。

時間領域と周波数領域

電子回路を設計・評価する上で、信号を正確に観測することは非常に重要です。その代表的な計測器として、オシロスコープとスペクトラムアナライザが挙げられます。この2つの計測器はどちらも電気信号を視覚的に捉えるためのものですが、その表示方法や得意とする解析領域が異なります。オシロスコープが信号の「時間的な変化」を捉えるのに対して、スペクトラムアナライザは信号に含まれる「周波数成分」を解析します。

この違いを理解しないまま計測器を使用すると、信号の特性を正しく評価できなかったり、問題の原因を見誤ったりする可能性があります。そのためここではファンクションジェネレータを使っていくつかの代表的な信号を生成し、それをオシロスコープとスペクトラムアナライザで同時に観測することで、両者の見え方の違いを検証します。

入力インピーダンスの影響

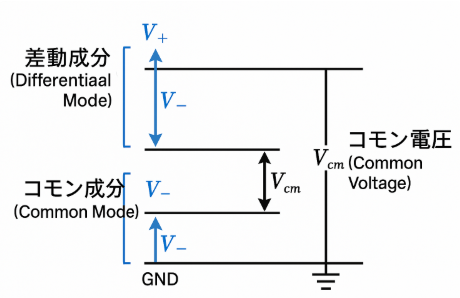
オシロスコープとスペクトラムアナライザは解析領域以外にも違いがあり、それが入力インピーダンスです。入力インピーダンスとは信号源から見たときの負荷（回路、計測器など）のインピーダンスのことで、用途によって適切な入力インピーダンスが異なります。

一般的な電気・電子回路の場合、対象とする信号の周波数が低いため入力インピーダンスが高いものが好まれます。入力インピーダンスが高くなることのメリットは信号の電圧降下を最小化できることです。ロー出し・ハイ受けと言われるように、出力インピーダンスが低く、入力インピーダンスが高い組み合わせが最も良いとされています。

一方で高周波回路ではインピーダンスの不整合によって信号が反射するため、出力インピーダンスと入力インピーダンスの大きさを一致させる必要があります。一般的には入出力インピーダンスは50Ωで統一されていますが、用途によっては75Ω、100Ω、150Ωなどの場合もあります。

オシロスコープの入力インピーダンス

オシロスコープの測定対象となる回路は一般的な電気・電子回路がほとんどです。そのためオシロスコープの入力インピーダンスは1MΩと非常に高く設定されています。これは、測定対象の回路にオシロスコープを接続した際に、できるだけ回路の動作に影響を与えないようにするためです。

スペクトラムアナライザの入力インピーダンス

スペクトラムアナライザは高周波信号を扱うため、入力インピーダンスは信号源と同じ50Ωに設計されています。信号源の出力インピーダンスと計測器の入力インピーダンスが等しい状態をインピーダンス整合（マッチング）と呼び、信号の反射が抑えつつ、信号源からのエネルギーが最も効率よく伝送できるようになっています。

インピーダンス不整合の影響と対策

ファンクションジェネレータ（50Ω）から出力された信号を、入力インピーダンスが1MΩのオシロスコープで測定する場合、インピーダンスは整合しません。これによって信号の反射が起こり、特に高い周波数では波形が乱れる原因となります。またオシロスコープで観測される電圧は、インピーダンスが整合している場合に比べて振幅が2倍になります。そのため高周波信号を精度良く測定するために、分岐コネクタを使ってオシロスコープに50Ω終端（ターミネータ）を接続してインピーダンスを整合させます。

図　オシロスコープに50Ω終端を接続している様子

正弦波の比較

はじめに最も基本的な信号である正弦波で比較します。ファンクションジェネレータから周波数10MHz、振幅-40dBmで正弦波を出力します。

図　ファンクションジェネレータの設定

オシロスコープによる測定

オシロスコープの画面には時間の経過とともに電圧が滑らかに上下する、おなじみのサインカーブが表示されます。ただし波形の残像が示すように、振幅の変動が生じており、これだけ見ると信号の出力レベルが安定していないように見えます。

図　オシロスコープで10MHzの正弦波を測定した様子

この振幅変動の理由は先に説明したインピーダンス不整合によって、信号に反射が生じるためです。分岐コネクタを使ってインピーダンス整合させているとはいえ、これはあくまでも簡易的な処置であり、高い周波数までインピーダンス整合させ続けることは困難であることが見て取れます。

スペクトラムアナライザによる測定

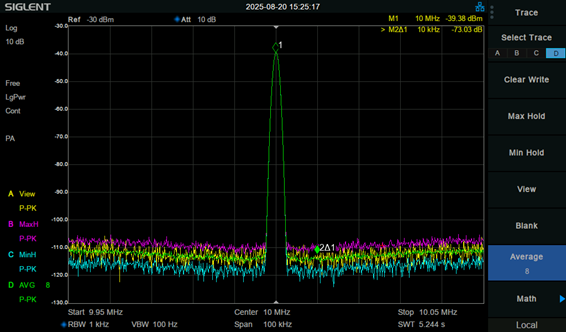
一方でスペクトラムアナライザではインピーダンス整合しているため、余計な反射なしに10MHz単体の信号として測定できています。また信号とノイズの差分を示すSN比も大きいため、信号の電圧や周波数の安定性を評価することも容易です。

図　スペクトラムアナライザで10MHzの正弦波を測定した様子

なお中心周波数の10MHzから一定の帯域幅を持っているようにも見えますが、これはスペクトラムアナライザの設定によるもので、分解能を高くするほど1本のスペクトルに近づいていきます。

また電圧変動だけに着目する場合はゼロスパン測定も有効です。ゼロスパン測定では特定の周波数の電圧の時間変化を測定できます。ただしオシロスコープのように高い周波数でサンプリングするわけではないため瞬時的な変動を測定することはできません。またスペクトラムアナライザは入力段のミキサーとフィルタによる帯域制限がかかるため、サインカーブも表示されません。

図　スペクトラムアナライザで10MHzの正弦波をゼロスパンで測定した様子

矩形波の比較

つづいて矩形波で比較します。ファンクションジェネレータから周波数10MHz、振幅-40dBm（4.4mVpp）で矩形波を出力します。デューティー比は50％と20％の2パターンで検証します。

オシロスコープによる測定

まずデューティー比50％の矩形波を測定してみると、正弦波のときと同様に反射の影響によって振幅の変動が大きくなっている様子が確認できます。ただし振幅のピークツーピークは4.6mVとおおよそ近い値を示しており、波形の傾向を確認する程度の測定には使えそうです。

図　オシロスコープで10MHzの矩形波（デューティー比50％）を測定した様子

次にデューティー比が20％にすると、信号の立ち上がりや立ち下がりのなまりも目につくようになります。これは10MHzの周期100nsに対してデューティー比が20％とすると、パルス幅は20nsとなりますが、この20ns幅に対して波形がなだらかになっていることが確認できます。このようにパルスの時間的な性質を評価するにはオシロスコープは最適で、高速信号に対してはアイパターンを用いて信号品質を評価したりもします。

図　オシロスコープで10MHzの矩形波（デューティー比20％）を測定した様子

スペクトラムアナライザによる測定

デューティー比50％の矩形波をスペクトラムアナライザで測定すると、10MHzを基本波として奇数次の高調波（30MHz、50MHz、70MHz、90MHz）が発生している様子が確認できます。

図　スペクトラムアナライザで10MHzの矩形波（デューティー比50％）を測定した様子

この高調波が発生する理由は、数学的に矩形波が正弦波の足し合わせによって表現できることから説明できます。

図　矩形波と高調波の関係

矩形波はデジタル信号のON・OFFによって生じますが、その波形をフーリエ変換すると複数の正弦波の足し合わせによって表されます。そしてデューティー比50％においては、基本波＋奇数次高調波として表され、高次の高調波成分が含まれるほど遷移時間が短い理想的か矩形波へと近づいてきます。これを周波数領域から説明すると、遷移時間が短いものほど高調波成分が多く、特にノイズ対策において波形をなまらせる手法が用いられるのはこのためです。

図　矩形波の遷移時間と周波数帯域の関係性

次にデューティー比20％では高調波が発生することは共通していますが、奇数次だけでなく偶数次の高調波も発生している様子が確認できます。これを周波数領域から説明すると、高調波成分の組み合わせによって矩形波のデューティー比を調整できると言えます。

図　スペクトラムアナライザで10MHzの矩形波（デューティー比20％）を測定した様子

チャープ信号の比較

最後により複雑な信号としてチャープ信号を測定してみます。チャープ信号とは時間とともに周波数が連続的に変化する信号です。ここでは1秒間で1MHz～10MHzまで周波数が上昇するチャープ信号を例にします。

オシロスコープによる測定

オシロスコープでチャープ信号を測定してみると、信号が時間的に変化している様子は確認できるものの、遷移する信号の周波数をリアルタイムに把握するのは難しいことが見て取れます。

図　オシロスコープでチャープ信号を測定している様子

ただしオシロスコープはサンプリングが1周期終わると、そこからデッドタイムによって信号を補足できない時間が生じるため、表示されている波形が必ずしもチャープ信号の全てを表しているわけではありません。

図　オシロスコープの取り込み時間とデッドタイムの関係

スペクトラムアナライザによる測定

スペクトラムアナライザは信号の周波数成分を測定するための計測器ですが、時間的に変化する信号の測定にはあまり適していません。実際にClear Writeのままチャープ信号を測定すると、信号をほとんど補足できません。これはスペクトラムアナライザとチャープ信号の掃引時間が一致していないためです。

図　スペクトラムアナライザでチャープ信号を測定した様子

この掃引時間の不一致による信号の欠落を補う方法として、最も簡単なのはMaxHoldを使用することです。MaxHoldは周波数ごとに最大値を記録しているもので、時間をかけるほどより多くの信号を補足できるようになります。ただしこれだけでチャープ信号を完全に保続することはできません。

図　スペクトラムアナライザのMaxHoldでチャープ信号を測定した様子

次の方法としてはRBWを大きくすることが挙げられます。RBWを大きくすると一回の測定で細く可能な周波数範囲が広がり、かつ掃引時間も早くなるため信号の捕捉率が高まります。ただしこの方法では周波数分解能が低下するため、測定の目的に適しているかどうかは十分検討する必要があります。また捕捉率が高くなるとはいえ、完全にチャープ信号を捉えられるわけではありません。

図　RBW100kHzでMaxHoldしてチャープ信号を測定した様子

このように掃引型スペクトラムアナライザでは原理的にチャープ信号の測定には適していません。そのためチャープ信号のような動的な信号に対してはFFT型のリアルタイムスペクトラムアナライザでなければ正確な測定はできません。その点でSVA1015XはSweep ModeからFFT型を選択できます。リアルタイムスペクトラムアナライザほどの捕捉率はありませんが、掃引型と比べると格段に捕捉率を高めることができます。

図　Sweep ModeをFFTに変更してチャープ信号を測定した様子

まとめ

オシロスコープは時間領域で信号の形を、スペクトラムアナライザは周波数領域で信号の成分を測定しています。その中で矩形波のように単純に見える波形も、実際には多くの高調波から成り立っていること、そしてチャープ信号のような動的な信号を捉えるには、スペクトラムアナライザの動作モード（掃引型・FFT型）の選択が重要であることがわかったはずです。

電子回路の設計やトラブルシューティングにおいては、この時間と周波数という2つの視点を自在に行き来する能力が非常に重要になります。オシロスコープで波形の乱れを見つけたら、スペクトラムアナライザでその原因となっているノイズの周波数を特定し、対策を講じる。このように両者を相補的に活用することで、より正確に信号の特性を理解し、高度な問題解決へとつなげることができます。